Next: 4. Phase Restrictions Up: Rotation Matrices and Translation Vectors in Previous: 2. The Structure Factor
![[IUCr Home Page]](/iucr-top/logos/iucrhome.gif)
![[Commission Home Page]](/iucr-top/logos/cteach.gif)
![]()
![]()
![]()
Next: 4. Phase Restrictions
Up: Rotation Matrices and Translation Vectors in
Previous: 2. The Structure Factor
In a space group with n equivalent positions (Rix +
ti), i = 1, 2, ![]() , n the structure factor can be calculated through
summing up the contributions to it in the following way:
, n the structure factor can be calculated through
summing up the contributions to it in the following way:
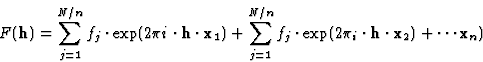 |
(4) |
According to (1) every equivalent position can be written as Rx + t. If this expression is inserted into (4), and we for the sake of simplicity look at a space group with 2 equivalent positions, we obtain:
![\begin{displaymath}
F(\textbf{h}) = \sum^{N/2}_{j=1}f_j \exp (2{\pi}i\textbf{hx}...
...\sum^{N/2}_{j=1}
f_j \exp (2{\pi}i\textbf{h}[\textbf{Rx} + t]).\end{displaymath}](img13.gif) |
(5) |
![]()
| (6) |
![]()
If (5) and (6) are combined we get:
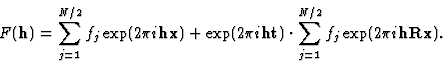 |
(7) |
Copyright © 1981, 1998 International Union of Crystallography
IUCr Webmaster